|
Superstring theory describes a world comprised of at least 10
dimensions. For most of us—with our way of thinking and the
way in which we experience the world—it's difficult to imagine
more than three spatial dimensions. In mathematics, however, working
in more than three spatial dimensions poses no problem at all and
helps solve problems not solvable otherwise. Here's a simple example
that shows why.

|

|
|
Dimensionless point
A point has no width, no height, and no depth. It has no
dimensions and so no numbers are needed to describe it. We
could describe a location where a point exists with numbers if
we wanted to give its position, but right now we're only
concerned with the point itself.
|

|

|
|
One-Dimensional Line
A one-dimensional line can be described by one number, which
describes the line's length. Length can be measured in any of
a number of units—inches, centimeters, finger widths,
etc. This one is measured in pixels.
|
|

|

|
|
Two-Dimensional Rectangle
The rectangle can be described by two numbers. One number is
length (the first line), and the other is height. By
multiplying these two numbers, you can find the area of the
rectangle.
|

|

|

|

|

|

|

|

|

|
| |
|
|
|
length
|
*
|
height
|
=
|
area
|
| |
|
|
|
100 pixels
|
*
|
50 pixels
|
=
|
5,000 square pixels
(or pixels2)
|
|

|
|
|
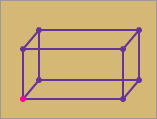
Three-Dimensional Box
This box can be described by three numbers: length, height,
and depth. By multiplying these three numbers, you can find
the volume of the box.
|

|

|

|

|

|

|

|

|

|
| |
|
length
|
*
|
width
|
*
|
depth
|
=
|
volume
|
| |
|
10 pixels
|
*
|
20 pixels
|
*
|
55 pixels
|
=
|
125,000 cubic pixels
(or pixels3)
|
|

|
|
|
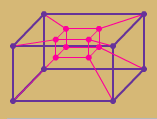
Four-Dimensional Hypercube
A hypercube is created by pulling the box into a fourth
dimension—into a space that we cannot experience. It is
difficult to imagine a four-dimensional object (and to depict
one on the two-dimensional surface of a computer screen), but
in this case focus your attention on the mathematics involved.
The formula (expression?) below describes the total
volume—hypervolume—of an object that exists in
four spatial dimensions.
|

|

|

|

|

|

|

|

|

|
|
length
|
*
|
height
|
*
|
depth
|
*
|
hyperdepth
|
=
|
hyper volume
|
|
10 pixels
|
*
|
20 pixels
|
*
|
15 pixels
|
*
|
60 pixels
|
=
|
7,500,000 pixels4
|
|

|

|
|
Is the Expression Meaningful?
Although it's difficult to imagine a four-dimensional object,
the "pixels4" resultant of the equation is
meaningful. If there was another four-dimensional box just
like the one shown here, but was deeper into the fourth
dimension, the hyper volume measurement of the object would be
larger. This number would be useful for comparing the "size"
of the object to that of another.
Likewise, the math involved with string theory is meaningful
(at least in the mathematical sense), although the objects it
describes are much more complex and much more difficult to
imagine. Shown here is an attempt. This is a rough
representation of a so called Calabi-Yau shape. Its six
dimensions, along with the three familiar spatial dimension
and the dimension of time, account for the 10 dimensions of
string theory.
|

|

|

