The Proof

Student Handout

When is a Line Not a Line?

Mathematicians like Andrew Wiles, who proved Fermat's Last Theorem, rely on complex mathematics to prove something. While his theories dealt with elaborate mathematics, you can investigate some more basic mathematics principles here.

Part I
Write your answers on a separate sheet of paper.

1. Begin by drawing a horizontal and vertical axis on the graph paper. Mark eight points on each axis, each one inch apart. Label each axis with eight numbers as shown. These are the draw points.

   
   
   

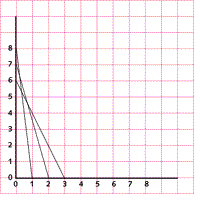
2. Use a ruler to draw a line from point 8 on the vertical axis to point 1 on the horizontal axis.

3. Next, draw a line from point 7 to point 2. Continue drawing lines between the descending vertical points and ascending horizontal points until all eight points have been connected. Use a ruler as you draw so that the lines connecting the points are straight.

   
   
   

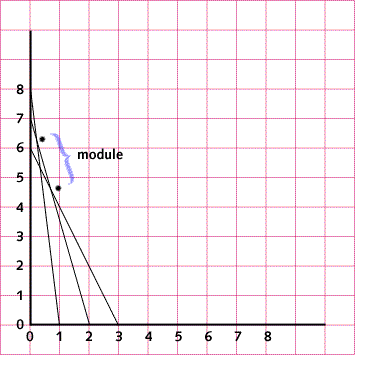
4. As each connecting line intersects, a shape is formed. Describe this shape.

5. Notice that the shape is made of small straight lines. Each of these straight lines is called a module. Measure and record the length of each module in your shape.

6. Compare the length of each module. Is each module length the same or different? Describe any pattern you notice.

Part II
Write your answers on a separate sheet of paper.

1. Try changing the grid in one of the following ways:

   1. increase or decrease the distance between the draw points.

   2. use an odd number of draw points.

2. Choose your new distance between draw points, or the number of draw points you want, and create a grid as you did in Part I.

3. Describe the shape that results from the intersection of the lines. Measure and record the module lengths along these curves.

4. Describe the pattern you notice among the sequence of modules.

5. Compare your new grid to the first grid you made. How are they alike? How are they different?