
|
|
Einstein's Big Idea
|

|
|
Classroom Activities
|
Squaring Off With Velocity
|
Activity Summary
Students investigate the meaning of c2 in
E = mc2 by measuring the energy delivered by an
object falling at different velocities. Graphing data leads students
to understand that E
is proportional to velocity squared, not simply velocity.
Learning Objectives
Students will be able to:
-
explain what the c2 in
E = mc2 represents.
-
state that kinetic energy is the energy of an object in motion.
-
illustrate how kinetic energy can be transferred to other
objects.
-
understand that the energy delivered by an object in motion is
proportional to v2, not v.

-
copy of the "Squaring Off With Velocity" student handout (PDF
or
HTML)
-
copy of the "Data Sheet" student handout (PDF
or
HTML)
- 1 lb flour in a plastic bag
- plastic pan (about shoebox size)
- two 8-oz plastic cups
- four standard-sized (about 1 cm) glass marbles
- plastic ruler
- meter stick
- plastic spoon
- wood dowel or wood barbecue skewer
- felt-tip pen
- graph paper
- newspaper
Background
Light has fascinated scientists for centuries. Galileo Galilei was
the first to consider measuring its speed. In 1676, astronomer Ole
Roemer made observations of the eclipses of Jupiter's moons to
demonstrate that light moved at a very fast—but not
infinite—speed. James Clerk Maxwell provided the mathematical
backbone for electromagnetism and demonstrated that light was an
electromagnetic wave. The squared part of Albert Einstein's equation
heralds back to natural philosopher Gottfried Leibniz, who proposed
that an object's energy is the product of its mass times its
velocity squared, not just its velocity. Emilie du Châtelet
further championed his ideas. While many of these scientists were
innovative thinkers, determination also played a large part in their
achievements. They were willing to challenge widely held beliefs of
their day. Their courage and perseverance helped lay the groundwork
for Einstein's eventual connection of mass, energy, and the speed of
light squared.
In this activity, students use a simple model to investigate the
relationship between velocity and energy. Their investigation leads
them to conclude that the energy delivered to a system depends on
the velocity squared of the impacting body, not simply on the
velocity. Students then relate this fact to
E = mc2.
The model uses a glass marble as a falling object that impacts a cup
of flour. The impact velocity of the marble is a function of the
height from which the marble is dropped. The energy released by the
falling marble (its potential energy now turned into kinetic energy)
is equal to the work done on the flour. The work done on the flour,
in turn, is equal to the force (mass x deceleration) it takes to
slow the marble down to zero velocity over the distance it
penetrates the flour.
Four heights are used-10, 25, 50, and 100 centimeters. Students
graph the velocity the marble attains when dropped from these
heights against the depth to which the marble penetrates the flour.
The depth, in turn, is a measure of the energy that the marble
delivers. Students can calculate the impact velocity at these four
heights by using the equation:
![v = [radical]2gd](/wgbh/nova/teachers/activities/images/3213_velocity.gif)
where g = the acceleration due to gravity (9.8
m/sec2), and d = the distance the marble falls (in
meters)
Key Terms
kinetic energy: Energy of a moving object.
speed: The rate at which an object moves.
velocity: The speed and direction of a moving object.

Assemble all the materials needed for the activity. -
Write E = mc2 on the board and ask
students what the three letters in the equation represent.
Emphasize that c stands for a particular constant speed
or velocity, that of light in a vacuum.
-
Demonstrate the parts of the apparatus students will use to find
the relationship between E and v (a replacement in
the model for c). Marbles must be dropped from rest, and
the depth to which the marbles penetrate must be measured with a
dowel or skewer marked off in centimeters. The depth should be
measured from the top of the marble to the top of the flour. The
cup must be picked up, and the skewer must be viewed from the
side to measure depth accurately. Students should add a half
centimeter to their measurements in order to measure to the
marble's center of mass.
-
Organize students into teams. Distribute the student handouts
and materials. Assign teams to one of the four heights from
which to drop marbles. To ensure data reliability, have several
teams perform the same measurements multiple times and average
the results. As a class data table is going to be made, the more
data points the better.
-
Have students place newspaper on the floor, then place their
cups filled with flour in the center of a plastic pan. If
students run out of clear area in which to drop the marble, have
them scoop out the marble(s) with the plastic spoon, use the
spoon to refill the cup, tap the base of the cup three times to
remove air pockets, and then use the dowel to level the flour to
the cup's rim. If students' fingers plunge in to retrieve
marbles, they will pack down the flour and their next set of
data will be skewed with lower penetrating distances. Results
will also be skewed if they leave air pockets in the flour.
-
Ask students how they might find the velocity of the marble as
it hits the flour. When they arrive at the correct mathematical
strategy
![v = [radical]2gd](/wgbh/nova/teachers/activities/images/3213_velocity.gif)
have students calculate the velocity values for the four given
heights. (Students will need to convert centimeter drop heights
to meters.) Students may notice that doubling the height from
which they drop the marble does not double the velocity. If the
calculations are too rigorous for students, provide them with
the values for velocity (see
Activity Answer) and tell students to
square them for the v2 column of their table.
-
When student teams are finished, create a class data chart on
the board and have students fill it in or have them enter their
data into a computer spreadsheet.
-
This is an ideal time to do some data analysis and statistics.
Student answers may vary quite a bit. For a given distance, ask
students which of the data points are "wrong" and which ones are
"right." Discuss the best way to average the numbers so students
can graph just one depth for each distance dropped. Cross out
the two highest and lowest points (outliers) and average the
rest. Have students average all teams' depth results to
determine final class averages for each depth. Have students
enter the results in the depth column in the "Velocity vs.
Energy Data Table" on their "Data Sheet" handout.
-
Discuss factors that may cause data to vary, i.e., non-uniform
density of the flour, problems with measuring depth, variations
in tick marks, etc. Emphasize that while accuracy is important,
measurements may include a degree of error. The goal is to see
the pattern the data set (that energy is proportional to
velocity squared, not velocity).
-
Tell students they will make two graphs, the first with the
y-axis labeled Velocity (meters/second) and the
x-axis labeled Energy (depth in centimeters). The second
graph will have the y-axis labeled Velocity2
(meters2/second2) and the x-axis
labeled Energy (depth in centimeters). Meters are used on
the velocity axes to simplify graphing. Note that 0,0
must be used as a data point when drawing the curve.
-
Have students plot the first graph. When students have finished
plotting points, review how to interpolate and draw a curve
through a set of points instead of drawing "dot to dot," as
students will often do. Discuss the fact that a curve shows that
the two variables are not directly proportional.
-
Now have students plot their second graph in which the velocity
is squared. After students finish their second graph, help them
draw a straight line through as many points as possible. They
should try to have roughly the same number of points on either
side of their lines. Then have student teams answer the
questions on their "Data Sheet" handout. Review answers as a
class. What is the most noticeable difference between the two
graphs?
-
As an extension, have students use
![v = [radical]2gd](/wgbh/nova/teachers/activities/images/3213_velocity.gif)
to calculate from what heights marbles would need to be dropped
to double the velocity for each height (beginning with the
10-centimeter height). Have the students repeat the
experiment at this new set of heights (you may need to use very
wide-mouth cups in order for students to hit the target flour).
Extend the heights above the flour to 2 meters. Stop taking data
when the marble hits the bottom of the cup. Direct students to
plot this new set of data, compare it to their previous graphs,
and find the slopes for each line. Are they the same? Have
students explain their results.

Marbles dropped from different heights accelerate toward the surface
of the flour, increasing their velocity and kinetic energy as they
fall. The kinetic energy that the marble has gained is then
transferred to the flour as it plunges in. The depth that the marble
reaches in the flour is a measure of the kinetic energy that is
transferred to the flour (the energy deforms the flour and makes the
marble crater).
Student results may vary due to differences in flour density and
errors in dropping the marble from prescribed heights. When
reviewing the table with students, it would be best to eliminate the
two lowest and highest values for each height and average the rest.
The summary data plotted should reveal that energy is proportional
to velocity squared.
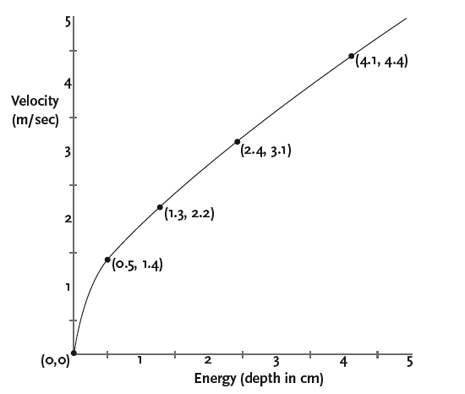
Sample Results
Velocity vs. Energy Data Table
|
Distance (cm)
|
v (m/sec)
|
v2 (m2/sec2)
|
Depth (cm)
|
|
0
|
0
|
0
|
0
|
|
10
|
1.4
|
2.0
|
0.5
|
|
25
|
2.2
|
4.9
|
1.3
|
|
50
|
3.1
|
9.8
|
2.4
|
|
100
|
4.4
|
19.6
|
4.1
|
The average error of the depth data was about +/- .5 cm.

Student Handout Questions
-
What is the shape of your Velocity vs. Energy graph?
The shape of the graph is a curve.
-
What is the shape of your Velocity2 vs. Energy
graph?
The shape of the graph should be close to a straight line.
-
If a straight line on a graph indicates a direct relationship,
is energy (measured by depth) directly proportional to velocity
or velocity squared?
The Velocity2 graph appears to show that energy is
proportional to velocity squared, not velocity.
-
Explain why Albert Einstein wrote
E = mc2 instead of E = mc.
Students may forget that the c is simply the velocity
of light. Einstein wrote c2 because
E is directly proportional to velocity squared, not
velocity.

Web Sites
NOVA—Einstein's Big Idea
www.pbs.org/nova/einstein
Hear top physicists explain E = mc2, discover the legacy of the equation, see how much energy matter
contains, learn how today's physicists are working with the
equation, read quotes from Einstein, and more on this companion Web
site.
Answers from Scientists
www.skirball.org/exhibit/einstein_answers_light.asp
Answers several questions related to light and
E = mc2.
The Electromagnetic Spectrum
imagers.gsfc.nasa.gov/ems/waves3.html
Describes the electromagnetic spectrum and includes information on
visible light.
The Ultimate Physics Resource Site
serendip.brynmawr.edu/local/IIT/projects/Glasser.html
Includes physics links and activities.
Books
40 Low-Waste, Low-Risk Chemistry Experiments
by David Dougan. Walch Publishing, 1997.
Includes introductory labs on measurement, density, temperature,
relative mass, and more.
Energy by Jack Challoner. Dorling Kindersley, 1993.
Surveys various sources of energy and the ways in which they have
been harnessed.
Light
by David Burnie. Dorling Kindersley, 1999.
Explains many aspects of visible light and other forms of
electromagnetic energy.
Stop Faking It!: Light
by William C. Robertson. NSTA Press, 2003.
Provides information and activities to help teachers and students
understand light.

The "Messing With Mass" activity aligns with the following National
Science Education Standards (see
books.nap.edu/html/nses) and Principles and Standards for School Mathematics (see
standards.nctm.org/document/index.htm).
Grades 5-8
Science Standard
Physical Science
Mathematics Standard
Measurement
Grades 9-12
Science Standard
Physical Science
- Conservation of energy and the increase in disorder
Mathematics Standard
Measurement
Classroom Activity Author
Jeff Lockwood taught high school astronomy, physics, and Earth
science for 28 years. He has authored numerous curriculum projects
and has provided instruction on curriculum development and science
teaching methods for more than a decade.
|

|
The need for c
c
is necessary in Einstein's equation because whenever part of
any piece of matter is converted to pure energy, the resulting
energy is by definition moving at the speed of light. Pure
energy is electromagnetic radiation—whether light or
X-rays or whatever—and electromagnetic radiation travels
at a constant speed of about 300,000 kilometers per second.
The speed of light must be squared because of the nature of
energy. When something is moving four times as fast as
something else, it doesn't have four times the energy but
rather 16 times the energy—in other words, that figure
is squared. So the speed of light squared is the conversion
factor that determines just how much energy lies within any
type of matter.
|
|







