Back to Teachers Home

NOVA scienceNOW: Profile: James McLurkin

Viewing Ideas

Before Watching

1. Many of your students have never experienced life without computers. Help them develop a clearer understanding of their personal, and society's, dependence on computers. Have them brainstorm a list of the ways computers are used today. Ask them: What roles do computers play in our lives? (Some examples include personal computers that help us write research papers or e-mail, calculators that make number crunching quick and easy, and computer chips that help our cars, microwave ovens, VCRs, cell phones, and other appliances run.) How would our lives change if computers did not exist?

   Then, have students brainstorm a list of city and state agencies with back-up systems that allow them to continue to provide critical services in the event of a power or computer failure (airlines, hospitals, nuclear power plants, fire departments, etc.).

   Finally, you might also have students interview older caregivers or friends, asking how they perform tasks for which we now use computers.

2. It used to be that Christmas tree light strings were wired bulb to bulb. If any bulb burned out, the whole string went dark. The more bulbs in the string, the more likely the string would fail because the additional bulbs meant more chances of failure. One of the first electronic computers was ENIAC, first operated on behalf of the U.S. Army in 1944. Like the old Christmas tree lights, ENIAC's 19,000 vacuum tubes were a constant source of failure. Technicians continuously circulated among its banks to change burned-out tubes as it operated. Help students understand how parallel and series circuits work.

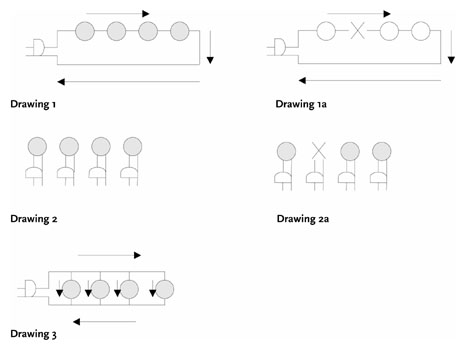
   Sketch Drawing 1 on the board. Have students trace the flow of electricity from one blade of the plug through all four light bulbs and back to the other blade of the plug. Next, erase one of the bulbs and replace it with a large X (see Drawing 1a). Ask whether the other bulbs would be able to light. (No.) Ask why all bulbs would be dark. (Pathway is broken.) Explain that this is a series circuit. Ask students to theorize why early versions of ENIAC would only run for about 20 minutes before a failure. (Many vacuum tubes create many opportunities for the pathway to break.)

   Sketch Drawing 2 next to Drawing 1. Explain that each bulb has its own plug. Now, erase one of the bulbs and replace it with a large X (see Drawing 2a). Ask whether the other bulbs would be able to light. (Yes.) Ask why the other bulbs would light. (They are on separate pathways.)

   Ask students to design a circuit that has only one plug, but all bulbs have a separate pathway to that plug. Have students share their designs. Sketch Drawing 3 after students have had a chance to try the challenge.

   Explain that Drawing 3 shows a parallel circuit. Ask students which circuit, series or parallel, is most likely to stay lit if a bulb burns out. Explain that James McLurkin designs computers that are made of many small computers working together. Ask whether McLurkin's computer robots are more like a series or a parallel circuit. (Parallel: Many robots represent many pathways to accomplish a task; when one fails, the others continue the task.)

   

3. Today, computers seem to effortlessly perform very complicated tasks. These tasks are actually based on thousands or even millions of simple step-by-step instructions painstakingly written by computer programmers. A single bad or missing instruction reveals that computers are really just mindless devices.

   List the following common tasks on the board: making a peanut butter and jelly sandwich, making chocolate milk from syrup, and brushing your teeth. Divide your class into four-member teams. Have each team choose one of the tasks. Explain that each student should write a set of instructions to successfully complete the chosen task. To simulate programming commands, tell students to write brief but clear instructions with only one action per line. Tell the teams that when they finish, each writer should read his or her instructions one step at a time while another team member acts them out. The remaining team members should look for any missing instructions or instructions that can be misinterpreted. For example, "Put the peanut butter on the bread" could lead to a jar sitting on an unwrapped loaf of bread. Ask teams to share some of the hilarious programming errors that they detected. In what ways is programming easy and difficult at the same time? How might you keep track of the instructions in a program that contained 1,000 lines?

After Watching

1. James McLurkin says the first rule about robots is that they are "profoundly stupid." They must be carefully and painstakingly programmed to be successful. His robots were unable to complete a music demonstration because of a programming error. Ask students to give examples of robots they are familiar with from books, television, and movies. How do McLurkin's real-world robots compare with these fictional robots?

2. McLurkin is very careful and schedules every detail of his activities on his computer, but it doesn't always help him stay on schedule. Why does this happen? Have students create flowcharts (or a step-by-step pictorial representation) of their day. First, discuss different ways students can create a flowchart. (It could be simply a series of boxes containing times and tasks connected by arrows.) Ask them to make a flowchart that includes everything they think they will do the next day. The flowchart should be fairly detailed. As they go through the day, have them keep a timed log of what they actually do. Then, have them compare the real-life log to their flowchart. Were they behind? Were they ahead? On schedule? Was there duplicate effort or unnecessary tasks? What adjustments do they need to make in their schedules to make their days more efficient and the flowchart more accurate? Make a new flowchart for the following day and test it out. Did their efficiency increase? What was it like to have a flowchart for their life? How, if at all, did it change their life?

3. This activity demonstrates how a large number of students (computers) can be programmed so that simple arithmetic operations can be carried out without anyone coordinating the process. (You may want to review the Data Flow Diagram before doing the activity with students in order to see how information travels between groups of students in the activity.)

   • Put students into the following four groups:

     1. The Result
     2. First Number
     3. Second Number
     4. Operation

   • Tell the students that you will give them a copy of their group's written instructions to review. You will then say "RUN," at which point they should stand up and execute the written instructions. After their group has performed its task, they should continue to display the results so other groups can see them.

   • To "program" the groups, copy the Instructions for Groups (PDF or HTML) handout. Cut up each group's instructions and distribute it to the appropriate group.

   • Review each group's instructions with them and ask them to demonstrate their programming.

   • Give the First and Second Number Groups a number and the Operation Group an operation (for example, 14 - 8 = 6). Remember that the largest number that can be displayed by any group is twice its membership.

   • Explain that after this activity begins, students are not to communicate with each other. They are to carefully follow all of the programming (instructions), observe, and react.

   • Start the calculation by saying "RUN." Assist the first attempt, as necessary.

   • Once the groups have completed their programming, count the Result Group hands and share the original operation and the results. Repeat with a new arithmetic operation, as desired.

   After the first run, you can test the resiliency of your distributed computer by asking several students to sit down during a run. Does the computer adapt and correct for these losses? Ask students how James McLurkin's small computers are like this distributed class computer. How would using 24 distributed computer robots be more effective than a single, very smart robot mapping a cave system or looking for a lost child?