
|
|
|
||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Objective 


If students need guidance, you may want to clarify the following concepts:
perimeter: the distance around a polygon; the perimeter is
determined by the sum of the lengths of the sides of the polygon. 
For any circle, if you divide the circle's circumference by the diameter you will always get the same number, pi. Pi represents the ratio of the circumference of a circle to its diameter. Pi can be used to find the circumference and the area of a circle, if you know what the radius (r) of the circle is. The equations for determining those values are:
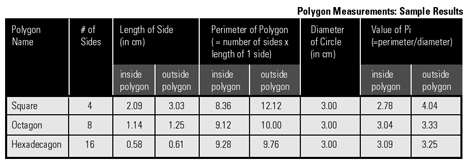
Circumference = 2 x π x r The concept of pi has fascinated mathematicians for more than 4,000 years, ever since people first noticed that the ratio of circumference to diameter was the same for all circles, regardless of the circle's size. Although earlier estimates of the value of pi exist, Archimedes seems to have carried out the first theoretical calculation of the constant. His approach consisted of inscribing and circumscribing regular, many-sided polygons in and around the circle, and computing the perimeters of these polygons. This provided him with the approximation 223/71 < π < 22/7, or 3.1408 < π < 3.1428. (The actual value of pi to four decimal places is 3.1415.) Pi is an infinite decimal; its value is currently known to more than 1 trillion decimal places. Archimedes did not have access to the modern-day tools of algebra, trigonometry, or even decimal notation. Instead, he performed his calculations using purely geometrical methods. Thus, constructing and calculating the values of the perimeters of 96-sided polygons, and then using these values to estimate pi, was by no means a trivial task. Students' answers should reflect that Archimedes' method gives an approximate range of values for pi, with the value from the inside polygon providing the lower boundary and the value from the outside polygon providing the upper boundary. In addition, students should discover that the more sides a polygon has, the better approximation of pi it provides. This is because a polygon with many sides gives a better approximation of the circumference of the circle than one with fewer sides. Students may wonder why it was so difficult to measure the circumference of a circle. The reason is that at the time Archimedes lived, there was no way to accurately measure curved lines—only straight lines could be measured. This is why Archimedes had to devise a way to approximate a circle's circumference. 
Book
Stein, Sherman.
Archimedes: What Did He Do Besides Cry Eureka?
Washington, DC: The Mathematical Association of America, 1999. Web Sites
Archimedes Home Page Find more resources in Links and Books online at www.pbs.org/nova/archimedes/ 
The "Archimedes' Recipe for Pi" activity aligns with the following National Science Education Standards and Standards for School Mathematics. Grades 5-8
Grades 9-12
|
|
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||