
|
|
Elegant Universe, The: Einstein's Dream
|

|
|
Classroom Activities
|
Background
String theory is elegant in a number of ways: it accounts for both
quantum mechanics and general relativity, it may have the potential
to describe the elementary particles that make up matter and carry
forces, and it provides a mechanism by which the four forces can be
unified. For these reasons, supporters of string theory are willing
to take on a daunting proposition—that the universe is not
actually made up of the four commonly experienced spacetime
dimensions, but may contain 10—perhaps even 11—spacetime
dimensions. Without these additional spatial dimensions, the
equations in string theory just don't work. This activity first
calls for students to imagine a world of fewer dimensions before
considering the idea of additional ones.
Objective
To visualize a universe with fewer than three spatial dimensions and
to consider how more than three spatial dimensions could exist in
the universe.

-
copy of the "Deducting Dimensions" student handout (PDF
or
HTML)


-
Have students read parts or all of Flatland by Edwin
Abbott, which provides an account of what life would be like in
Flatland, where the inhabitants are all geometric shapes living
in a two-dimensional world. This reading will give students an
image of a universe with fewer dimensions. You may want to have
students start at "Part 2: Other Worlds," which describes the
nature of one-, two-, and three-dimensional worlds.
-
Organize students into teams and distribute the "Deducting
Dimensions" student handout.
-
Have teams record the answers to the five bulleted questions for
the one- and two-dimensional universes they are imagining. Have
teams also record any additional observations or realizations
about these universes. Once they have finished, have teams
answer the two questions listed on the student handout.
-
When students have completed the activity, have teams report
their results. As students consider the perspectives of
inhabitants in a world with fewer dimensions, discuss with them
that these inhabitants would not likely be able to comprehend a
three-dimensional world, even though one exists. Point out to
students that just as the inhabitants of those universes would
have difficulty picturing extra dimensions, so it could be for
inhabitants of our world.
-
Discuss the idea of an additional six or seven spatial
dimensions with students (different string theories assume a
different number of added dimensions). Students may wonder where
these extra dimensions are and why they cannot see them. Explain
to students that some physicists believe these extra dimensions
occur at every point in the universe but are extremely tiny and
curled up. They are so tiny that they cannot be detected, even
with the most sophisticated research equipment.
To help students visualize this, you may want to have them
imagine how various three-dimensional objects (such as a
telephone cable or a clothesline) can seem at a distance like
they are one-dimensional (a line that can be traversed back and
forth). In these cases, two dimensions (side-to-side and
up-down) appear hidden, just as the added six or seven
dimensions in string theory appear hidden from view. (See
The Science of Superstrings
for an illustration of this concept.)
In Conclusion
Some physicists think that added spatial dimensions may take on
incredibly complex forms known as Calabi-Yau shapes. How the
dimensions are curled up, which physicists have not yet determined,
may establish the properties of elementary particles. Taking a
different tack, a few theoreticians propose that the extra
dimensions may be very large, even infinite, but cannot be seen
because all matter, as well as light, is trapped within the
dimensions of our universe; matter from other universes would appear
dark to us. In this theory, gravity is the only thing that escapes,
leading some physicists to suggest that this would explain why
gravity is by far the weakest of the four forces.

In a one-dimensional universe:
-
Creatures would have the form of a very thin worm, or a
point-like dot.
-
These creatures could not pass each other because that would
require a second dimension. So one creature could only see the
dot-like end of the next creature in front of or in back of it.
-
These creatures could only move forward until they bumped into
the creature in front of them and backward until they bumped
into the creature behind them.
-
These creatures could only pass messages from one to another
down the creature line (like in the game "Telephone").
-
Social structures would be limited to some number of inline-
communicating creatures. There might only be one large group, or
any number of smaller inline groups.
In a two-dimensional universe:
-
Creatures could have any shape—such as a square, triangle,
or circle—that is flat like a drawing.
-
Creatures would have both length and width, but not height.
-
One creature seeing another would see its companion as a line
and discern the other creature's shape by viewing the other
creature from various angles.
-
Creatures could move in any direction in their flat universe,
but because there is no up and down dimension, they would have
to move around each other.
-
As one creature moves around another, it could see the apparent
length (or size) of the creature change (unless the other
creature is circular).
-
Any creature could pass a message to any other that it could
move to.
-
Any number of social structures would be possible: singles,
tribes, or larger groups. The larger the group, the longer it
would take to get a message from one creature to another.
Assuming that nearly direct contact is needed to communicate, in a
one-dimensional world, a creature could only communicate with
another creature that is either directly in front of or in back of
it. In a two-dimensional world, if a creature is long and thin, it
could arrange itself with others like it in a group like the spokes
of a bicycle wheel so that any creature could communicate with any
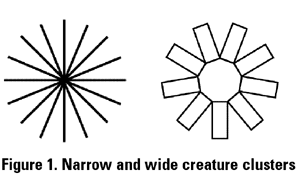
other across the center (see Figure 1). Wider—or myriad long,
thin creatures—could arrange themselves in a ring, but would
have to pass messages from creature to creature around the ring.
This loss of group contact would always occur at some number of
members within a cluster. The narrower the creature, the more
creatures that can remain in direct contact within a cluster.
In a one-dimensional world, the fastest way to communicate a message
to 64 creatures would be for the creature in the middle first to
tell the message to a creature on one side, and then to the creature
on the other side. These creatures would then relay the message to
the next two outside creatures, who would relay it to the creatures
outside of them, and so on, down each side of the line. The process
would take 32 minutes. In a two-dimensional world, the starting
creature would transmit a message to a second creature. The first
and second creature, then, would transmit a message to a third and
fourth creature. Then all four creatures would transmit the message
to four more creatures. This exponential transmission would continue
for six minutes, at which time 64 creatures would have heard the
message.

See the full set of
String Theory Resources

"The Elegant Universe" activities align with the following National
Science Education Standards.
Grades 9-12

|
Science Standard B:
Physical Science
|

|
Structure of Atoms:
-
Matter is made of minute particles called atoms, and atoms are
composed of even smaller components. These components have
measurable properties, such as mass and electrical charge. Each
atom has a positively charged nucleus surrounded by negatively
charged electrons. The electric force between the nucleus and
electrons holds the atom together.
-
The nuclear forces that hold the nucleus of an atom together, at
nuclear distances, are usually stronger than the electric forces
that would make it fly apart.
Structure and Properties of Matter:
|

|







