
|
|
Cracking the Maya Code
|

|
|
Classroom Activity
|
Activity Summary
Students see how scientists began to unravel the meaning of Maya
glyphs and then determine their own birth date using the Maya Long
Count calendar system.
Learning Objectives
Students will be able to:
-
explain some of the similarities and differences between the
Maya and U.S. mathematical systems.
calculate sums using Maya symbols. -
understand and use the Maya Long Count calendar system.

Multimedia Resources
Additional Materials
Background
The Maya civilization began about 2600 BC and thrived for more than
2,000 years. It reached its height of glory at about the same time
the Europeans were entering the Dark Ages (about AD 410). The Maya
were renowned for their monumental architecture, exquisite art, and
advances in mathematics and astronomy.
One of the most remarkable achievements of the Maya was their
complex calendar system. The Maya developed three types of
calendars, each serving a unique purpose:
-
The Tzolkin: A 260-day cycle used primarily for religious and
ceremonial events. It consists of twenty day-signs combined with
numbers from one to thirteen.
-
The Haab: A 360-day cycle for keeping track of seasons. The Haab
calendar consists of eighteen months of twenty days each, and
most closely resembles our solar year.
-
The Long Count: The longest-lasting cycle, lasting about 5,125
years. It signifies the length of a Creation period. We are
currently in the Fourth Creation, which began on August 13, 3114
BC and will end AD December 22, 2012.
When combined, the Tzolkin and Haab calendars could track 52 years
of time before day combinations began to repeat. This combination of
these two calendars was known as the Calendar Round.
Unlike U.S. mathematics, which works on a base 10 system, the Long
Count works on a base 20 (vigesimal) system. In the base 10 system,
a number in the first place is represented by numbers one to nine.
The second place value is 10 times the number in that place
(10)1, the third place value is 100 times the number
(10)2, and so on. In a base 20 system, the first place
value is represented by numbers one through nineteen, the second
value is 20 times the number (20)1, the third place value
is 400 times the number (20)2, and so on.
Many Maya structures feature engraved stone monuments, known as
stelae, that reveal the date the monument was built (visit
Decode Stela 3 to
see Maya and English translations of an actual Maya stela).

-
Have students view and take notes on the nine-minute
The Forgotten Maya Temples
video clip. Tell students they will learn about where the Maya
lived, what they were known for, and how scientists first
started to decipher Maya glyphs. Follow the video with a
discussion of the questions below:
-
Why is understanding original Maya writing important?
(Because it provides a picture of Maya history before the
arrival of Europeans.)
-
Where is the Maya region located?
(In the region extending from southern Mexico through
much of Central America.)
-
Why is it important to not rely solely on drawings in field
research?
(While drawings can be helpful, the person creating them
may introduce errors or omit important data when making
them. False conclusions may be drawn based on the drawing.
Photographs, [or when appropriate, field samples] provide
actual representations of an object under study.)
-
Write the following Maya symbols on the board. Tell students
that, like U.S. mathematics, Maya math uses a place value
system. The only difference is that the place value is
denoted vertically, rather than along a horizontal axis like
in the U.S. system. Review the places values for each level
and numerical values for each symbol (one dot = one; one bar
= five). Walk through the Column A problem and answer with
students and then have students calculate the solutions for
the other columns. (Column B = 26,981;
Column C = 98,663)
|
|
Column A
|
Answer
|
Column B
|
Column C
|
|
8000s
|
•
|
8,000
|
• • •
|
• •
|
|
|
|
|
|

|
|
400s
|
|
|
• •
|
•
|
|
|
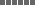
|
2,000
|
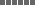
|
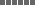
|
|
20s
|
• •
|
40
|
• • • •
|
• • •
|
|
|
|
|
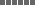
|

|
|
1s
|
• • • •
|
4
|
•
|
• • •
|
|
TOTAL
|
|
10,044
|
|
|
-
Tell students they will now learn how to calculate their date of
birth using one of the Maya calendar systems: the Long Count.
The Maya Long Count system uses a base 20 number system. Review
the difference between a base 10 system, which students are
familiar with, and a base 20 system. Read the student handout to
familiarize yourself with the calculations students will make.
-
Organize students in teams. Distribute copies of the
Calendar Count Worksheet
to each team.
-
Assist students in calculating their birth date according to
Maya Long Count.
-
As an extension, have student calculate how many days until the
Fourth Creation ends (December 22, 2012) and how many total days
are in the Fourth Creation.

Days from the beginning of the Maya Fourth Creation to December
31, 1987:
12.18.14.11.16 =
12 baktuns x 144,000 days = 1,728,000
18 katuns x 7,200 days = 129,600
14 tuns x 360 days = 5,040
11 uinal x 20 days = 220
16 kin x 1 day = 16
Total = 1,862,876
The number of days to each student's birth date will vary. Check to
make sure students include the extra day for each leap year, and the
day of their birth. Students will add the number of days from 1988
to their birth date to the number of days they converted in the
first part of the activity. Students will then use the conversion
chart to convert the number of total days back into Maya Long Count,
dividing first by the largest equivalent (baktun at 144,000 days)
successively down to the smallest equivalent (kin at 1 day).
The Fourth Creation will be completed on December 22, 2012, the Maya
date of 12.19.19.17.19. Scholars disagree on the precise correlation
of the Gregorian and Maya calendars. Their disagreements turn on
differences of days, however, not decades. (A correlation is
necessary to equate a Gregorian date with a Maya date; this means
finding a particular date that is identified by both systems.) For
this activity, the correlation for the most recent day of Maya Long
Count 0.0.0.0.0 is 584,285 days on the Gregorian calendar, thus the
first day of the Maya Long Count would be the 584,286th day on the
Gregorian calendar. This correlation is incorporated into all Long
Count calculations in this activity.

The "Calendar Count" activity aligns with the following Principles
and Standards for School Mathematics (standards.nctm.org/document/index.htm).
Grades 6-8
Number and Operations
Grades 9-12
Number and Operations
Classroom Activity Author
Written by Mary C. Turck. This classroom activity originally
appeared in the companion Teacher's Guide for NOVA's "Lost King of
the Maya" program.
|



|




